Online General linear equations calculator

The application General linear equations calculator let you find the solution of a system of linear equations.

In practice, several cases occur: system has 1. One solution, 2. Infinite solutions or 3. No solution.

1. If the system is well determined then it has one solution

Example:

3x + 2y = 2
x + y = 0

has solution x = 2, y = -2.

Popular calculators as CASIO fx-991/fx-570 can solve system of two or three equations: press [MODE] 5 EQN and then select 1 or 2. Enter 3 2 2 as the first equation and 1 1 0 into the second row then. When finished, get back by pressing [MODE] 1 COMP.

There are two approaches how to enter the above system on website Online & free linear equations calculator. The first approach is to enlarge the width of the table to three columns (i.e. to x, y, RHS). Then the values can be typed into the fields.

If the red handler located right from the table is being dragged, then the width accomodates the handler position, thus more column(s) appear or disappear. Set width such that complies to your needs.

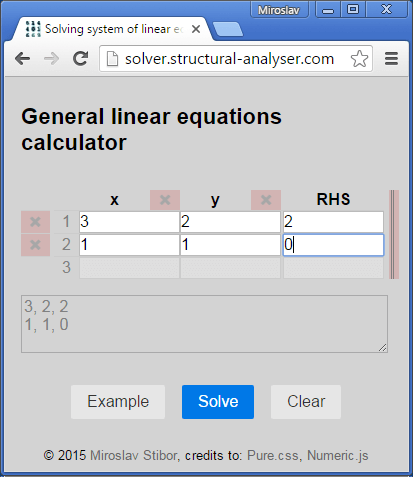
Let you type the values into the fields then. In our case two equations 3x + 2y = 2 and x + y = 0 are typed into the fields.

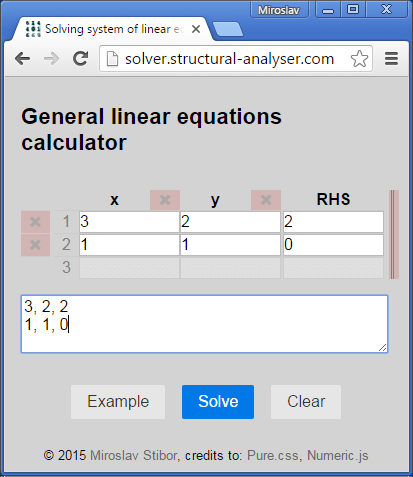
Alternative: you can skip all the above steps and edit the text field below the table. The values are separated by commas or by spaces. Each row is a line in the text field.

Finally the Solve button is pressed to obtain the solution x = 2 and y = -2.

2. If the system is not well determined then it has infinite solutions

That happens if there are less equations than unknowns or if some equations from the set are dependent. The determinant of the matrix = 0. Example:

3x + 2y = 2
6x + 4y = 4

has infinite solutions and it can be shown that the determinant of the left hand side (LHS) is 0. So not only x = 2, y = -2 is solution, also x = 0, y = 1 is.

It might appear that the two above equations bound well the solution but a further observation tells us there is in fact only one equation (as the second one from the set is a multiple of the first one and thus is not helpful). Oftentimes this dependency is not that obvious.

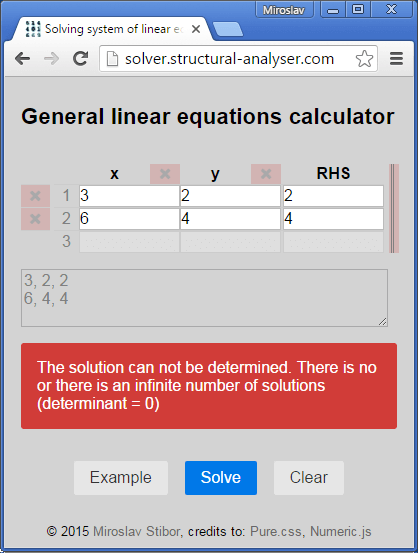
Determinant = 0 since the system of equations is not well determined and so has infinite solutions

3. A system has no solution if it is overdetermined

In this case only an approximate solution—which fits best all the given equations—can be found. In most cases the least squares method is employed to achieve that. Example:

3x + 2y = 2
x + y = 0
4x + 2y = 3

has no solution. A solution could be determined from the first two equations but it won't satisfy the last one. And so on. In real world it is common that the system is overdetmined and the task is carried then to find the best fit. There are many definitions what this best fit is. The most used criterion is that the solution is best fit if sum of squares Σ(RHS - LHS)² is at minimum (it is not the utmost best fit around but this definition is easy to describe and solve). That gives the best fit as x = 1.333, y = -1.111. If we substitute the best fit back into the set of equations, then we get

2.221 = 2
0.222 = 0
3.702 = 3

So it is not a solution indeed but it is close to it. Σ(RHS - LHS)² = (0.221² + 0.222² + 0.702² = 0.591). It is highly unlikely you would find a better solution (with the sum Σ(RHS - LHS)² smaller): the above solution was carried analytically (not shown here though).

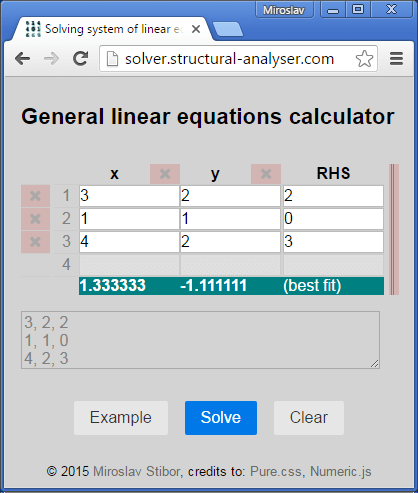
The system is overdetermined (more equations than unknowns) therefore has no solution. A best fit is kind of solution which doesn't satisfy all the equations but fits to the system of equations as best as possible.