Model considerations
A cantilever beam made from steel of length of 10 m will be modeled to simulate lateral torsional buckling (LTB). The dimensions of the cross section are shown later in the text.
Model is made from ANSYS 1D beam elements which implements also LTB. To have some comparison, two models will be made within the same project, each of them with different load. If the beam is loaded only by the buckling load, that means by a single force along the centroidal axis, there would be no LTB to be observed. There are more methods how to invoke buckling within the model.
- One of them is to make a buckling analysis and apply the natural shape obtained back to the structure (for buckling analysis).
- Or a small lateral load (perpendicular to the buckling load) can be used (used within this example).
Simulation
Preprocessor
Let us work with
- element type beam 188,
- Linear Isotropic Material EX = 210e9, PRXY = 0.3,
- Sections: beam (common section)
Subtype: T section
Dimensions as depicted on the picture
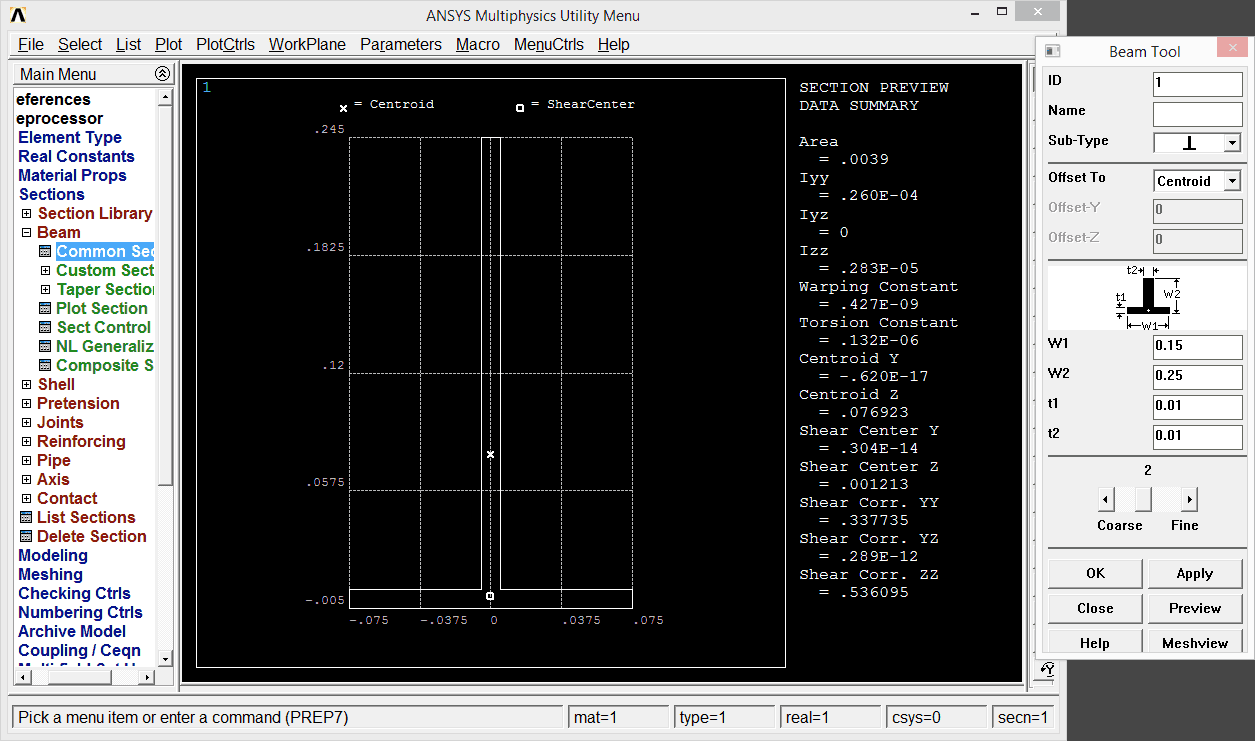
Important note: If we observe the section and its moments of inertia, then the buckling load has to come in direction of z coordinate.
Modeling: by two keypoints for one beam, and above them another two keypoints for a similar beam but with a different load:
k,,0 k,,10 k,,0,.5 k,,10,.5
Then lines
l,p
The above command's parameter p of line command stands for 'pickup by pointer'.
For meshing, let's first tell that we request 50 elements per line (per beam): go to Size cntrls/lines/picked lines: ndiv = 50. Then do the meshing itself: call Mesh/lines pick all
It is good idea to ensure that everything goes as expected by typing command elist in order to list all elements. Once the lines are meshed therefore elements are created, we can benefit from that: call command /eshape,1 to switch ON detailed shape of elements. After that let's redraw: from the menu Plot elements + from the menu PlotCtrls/Pan Zoom Rotate and select ISO view. Detailed 3D picture should appear as depicted on the screenshot:
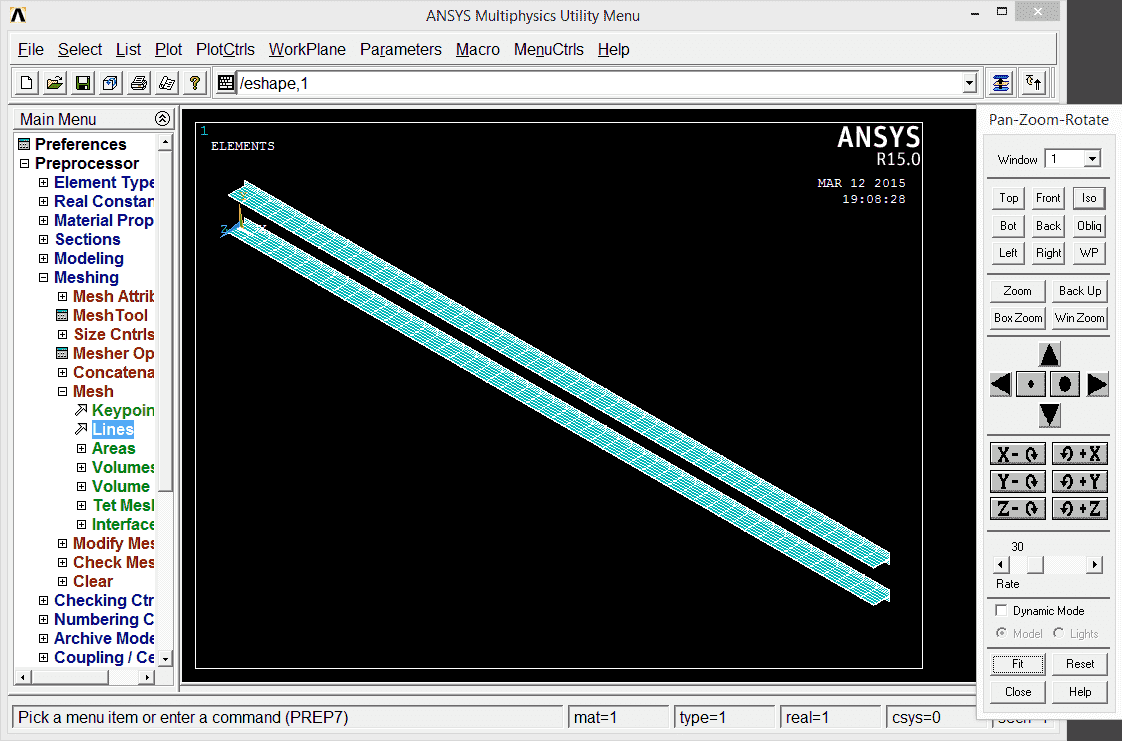
That view is also going to be helpful soon to realize the proper axes' convention when placing the buckling and lateral load.
The left support has to be a fixed support, therefore we define Loads/Apply/Structural/Displacement/On Keypoints (all DOFs). The buckling load will be placed on the right end: +5000 at z-direction (+4000 for the other beam).
To initiate buckling, let's place also a small lateral load: eg. +5 N along y axis (on both beams).
Solver
Now we can run the solver, but first we have to set up the task: it is going to be a static analysis with time increments (Solution/Analysis Type is static). During these time increments the load will be increased in steps, until the full value is reached.
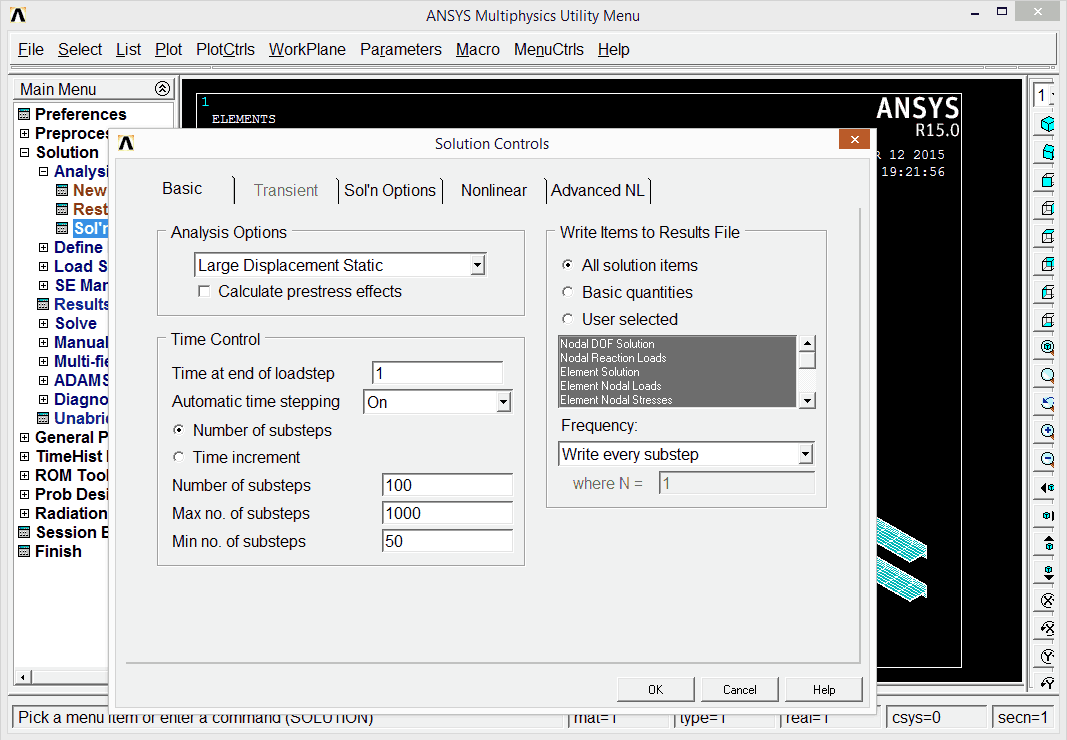
There are some more and less important settings within the solution Solution/Analysis Type/Sol'n Controls:
- Analysis options: Large displacement Static,
- Time at end of loadstep: 1,
- Automatic time stepping: O,
- Number of substeps: 100,
- Max no of substeps: 1000 (we do not want to wait indefinetelly),
- Min no of substeps: 50,
- Frequency: write every substep (otherwise only the last solution will be available for post processing).
These settings depend on the task; for a large structure a lot of steps will be time consuming. And if there are not enough steps, the solution might have difficulties to converge or can be faulty.
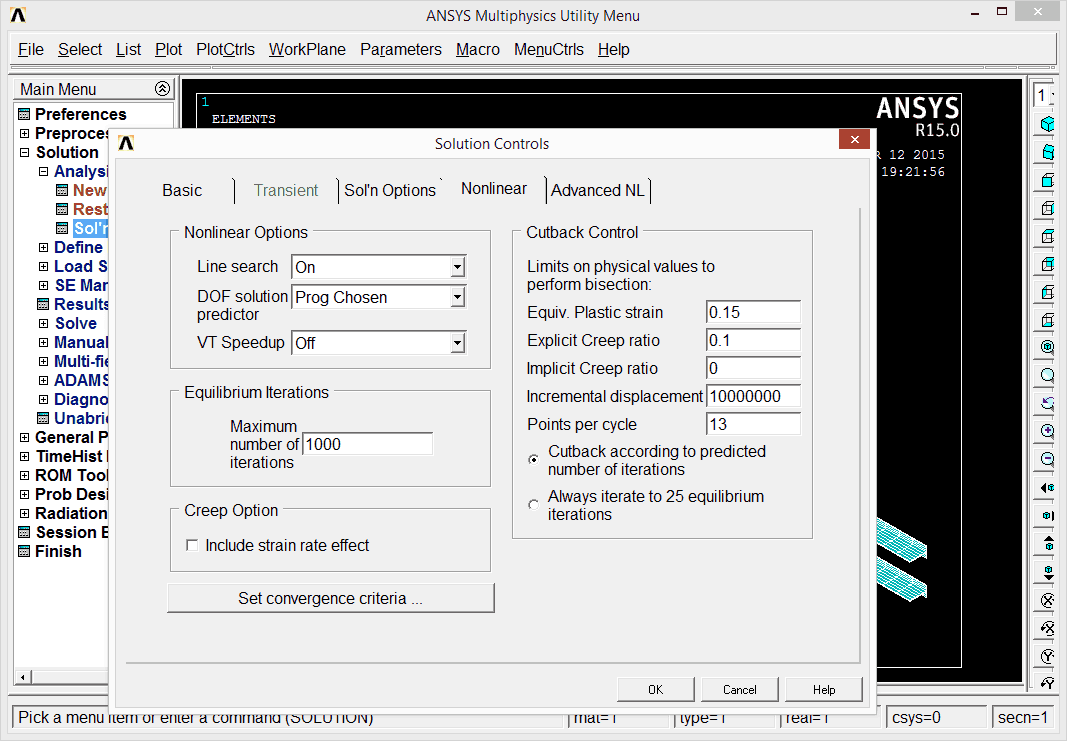
In the nonlinear tab:
- Line search: On,
- Maximum number of iterations: 1000.
Sometimes the solution does not converge. That usually happens for one of the two reasons:
- the load is to great, so the deflections are too large also and both the structure and solution become unstable: check the reaction at the last valid substep and fix the load accordingly (explained below);
- the time (so the load) increments are too great: increase the number of substeps.
The solver outputs a live chart, which is not much of our interest. These are informative values from the algebra behind the solver, with limited physical meaning. These lines trace how the solution converges.
Postprocessor
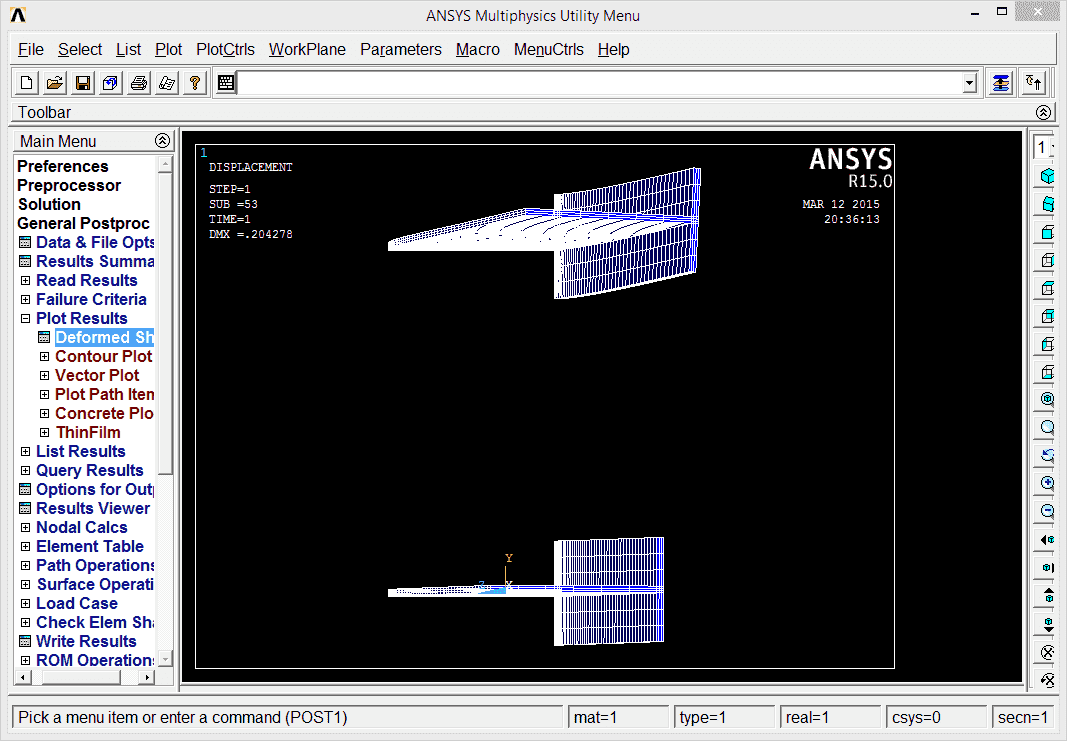
We can check all the solutions found (that means results at the end of each time increment) in General postproc/Results Summary. We can also pickup particular solution and explore that: General Postproc/Read Results/By Pick, then select an entry and press the button Read. The chosen solution can be explored for example by Plot results/Deformed shape.
Time History Postprocessor
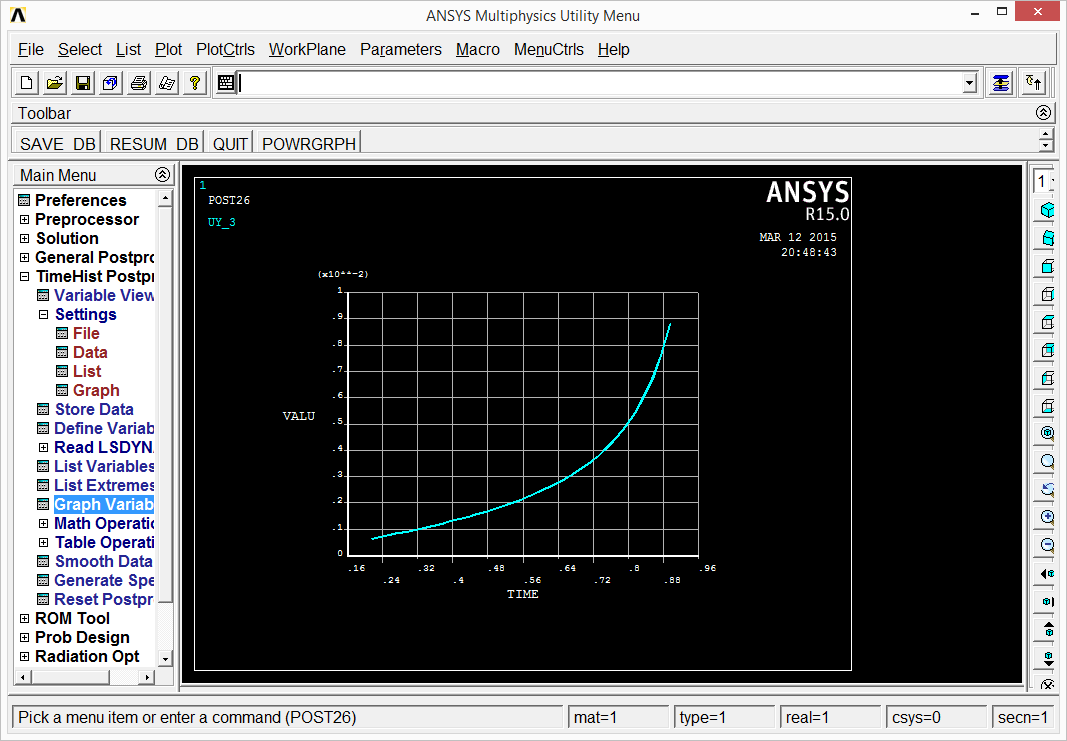
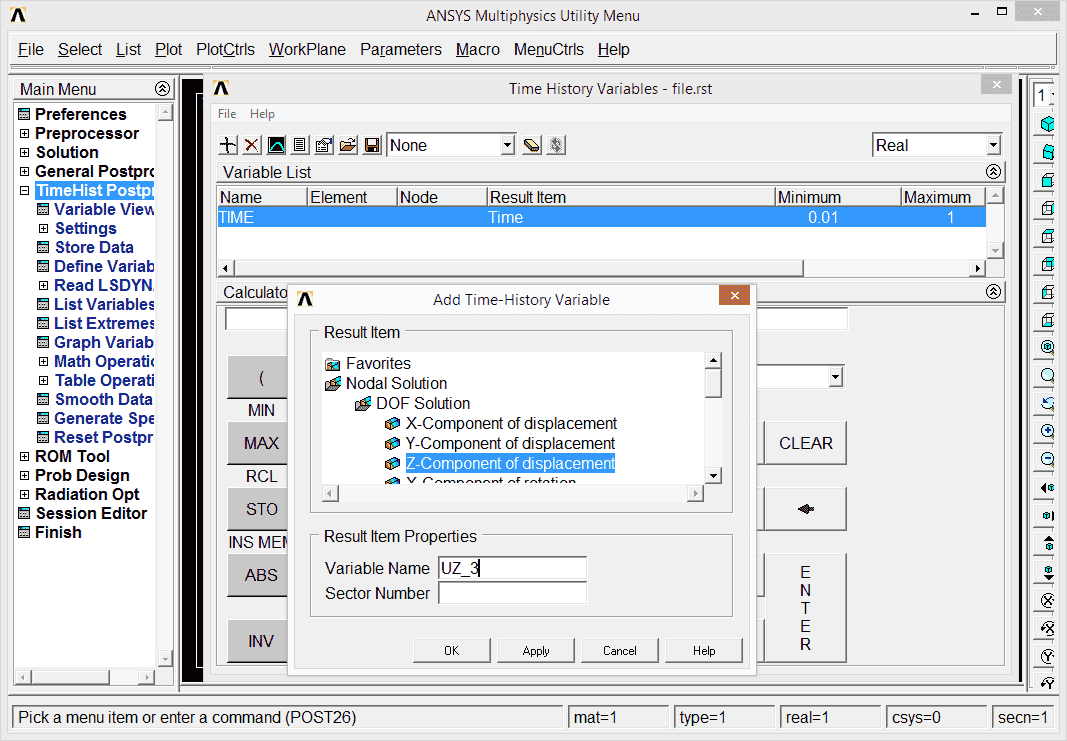
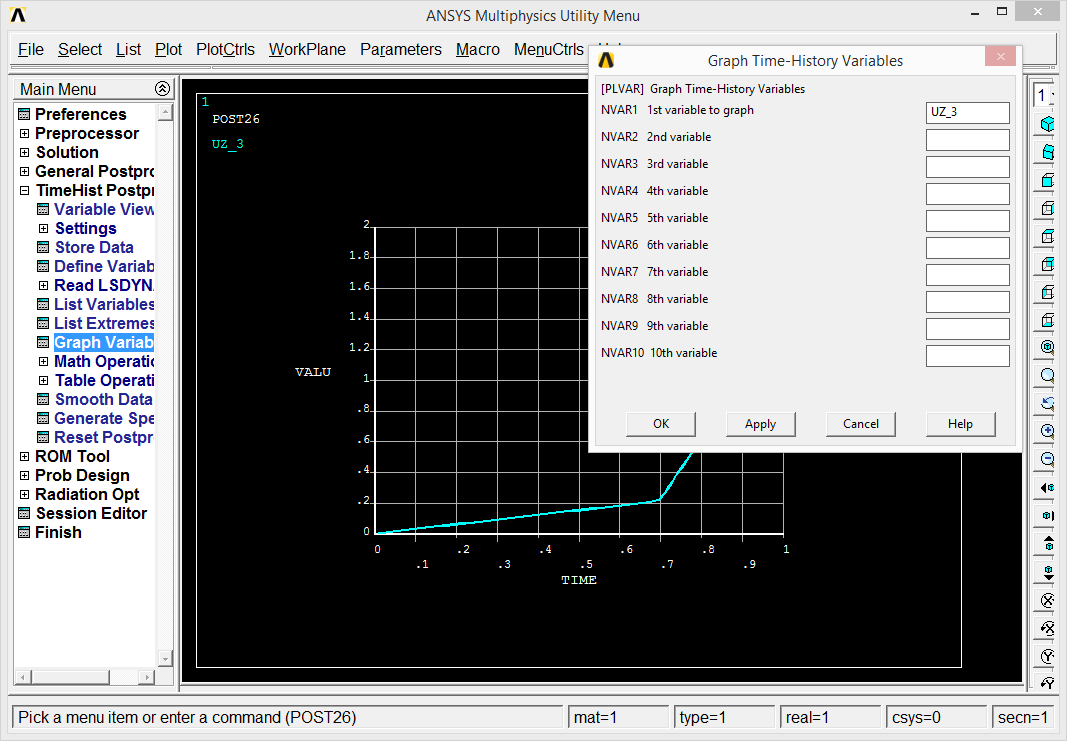
For buckling problems, we usually want to know when the instability starts to appear. So we want to observe results as a function of time (load). For that, let's go to TimeHist PostProc. We have to define new variable which can be plotted then. Add data (variable) and select DOF Solution Z-Component. New variable is given a name (UZ_3) which can be overwritten by user. ANSYS asks which node, so let's point to the right end node, which happens to be node 2.
The variable can be shown from Graph variable and it is UZ_3 to be drawn. It depends on interpretation but it can be observed that until time 0.85 s the beam appears to be stable and then the buckling starts to show up.
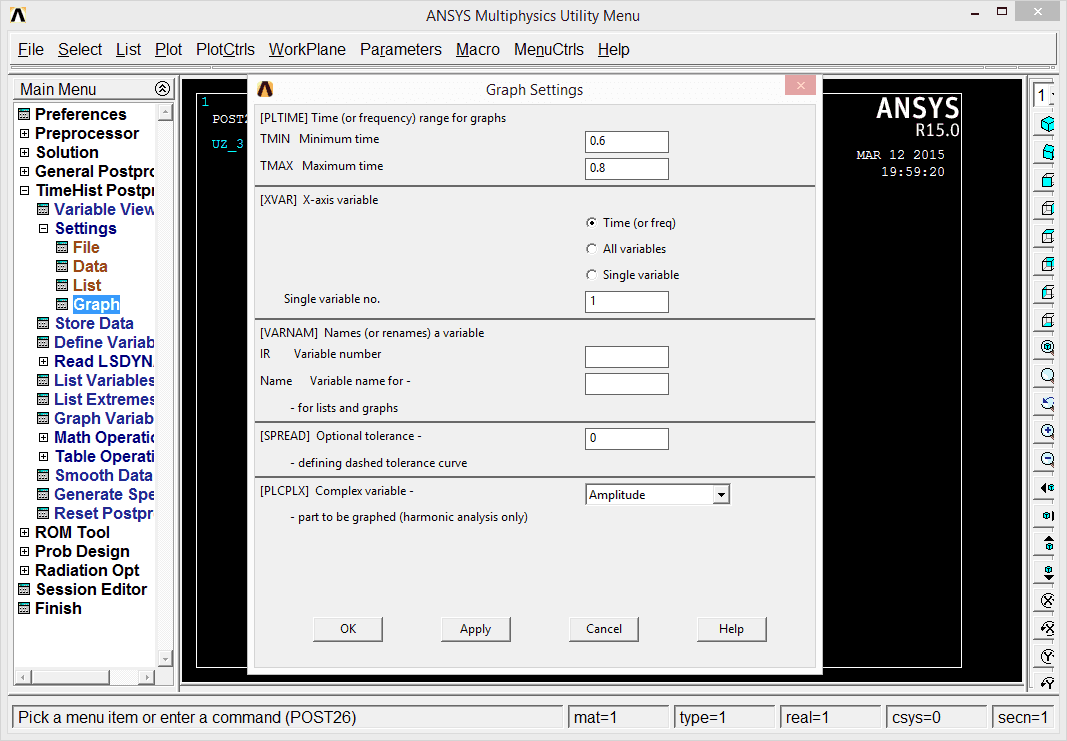
There are also settings to set limits to the time axis of the graph: go to TimeHist Postproc/Settings/Graph and set Minimum and Maximum time.
We can go to the time of 0.85 s to find the actual load. First let's make the proper solution active: one has to go to General Postproc and read results around time = 0.85 s and after some observations made it appears that the buckling starts at load of 4200 N.
Altering the model
Once finished, let's modify the model in order to find out, what would be the buckling load if it acts from the opposite direction. The ANSYS' GUI is more tricky compared to my online software, so it is worth to use FKLIST command to list all loads on all keypoints to modify them:
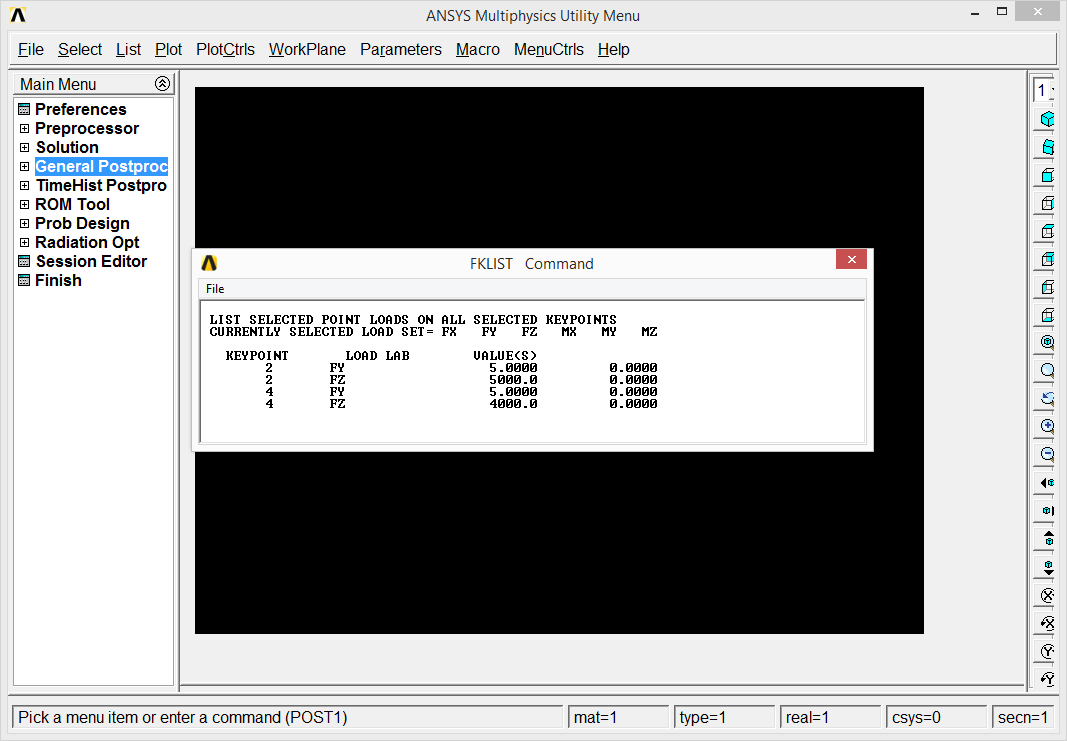
It appears that we want to modify FZ from 5000 N to -5000 N on keypoint 2 and from 4000 N to -4000 N on keypoint 4. Let's go back to Preprocessor to select entry Loads/Define Loads/Apply/Structural/Force/On Keypoints.
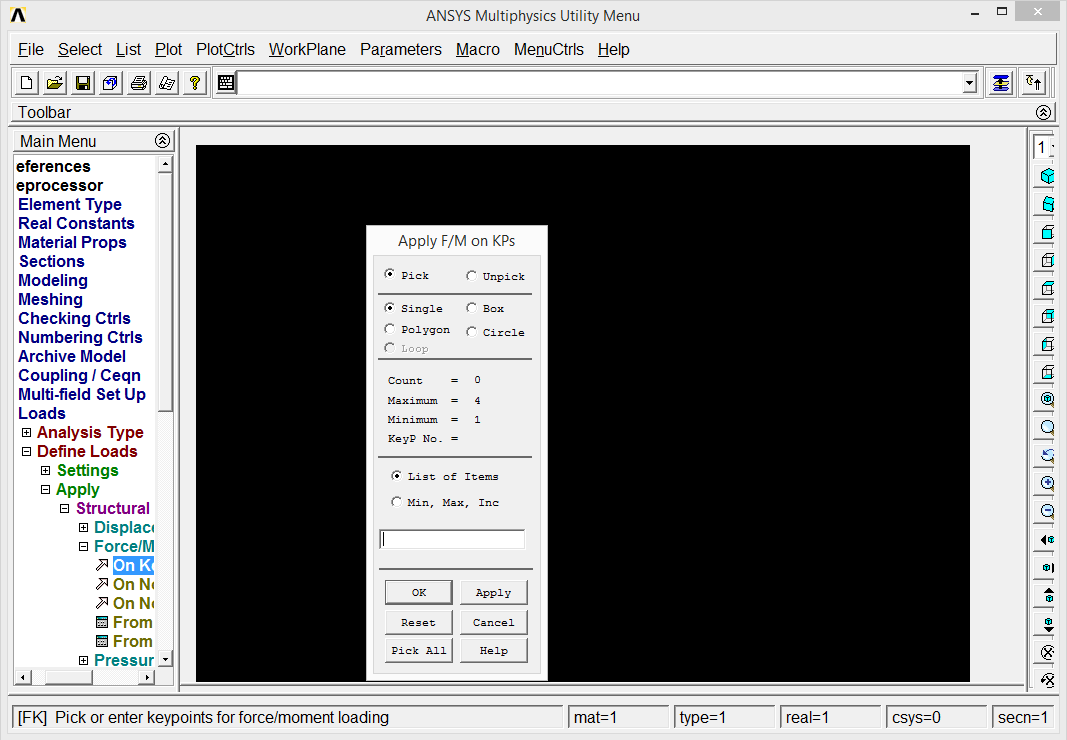
The dialog can be used to pickup the keypoint but let's rather enter its number (4) and press OK button, enter new FZ load of -4000 and do the analogy for the keypoint 2. It is good idea to check the modifications by FKLIST again.
It's time to call the solver again. It happens to me that this time solution does not converge. If I read the last valid step within the postprocessor, then I observe load at that time from reactions: looks that 4075 is a limit. So let's modify load to let's say -3500 and -4000 N. After repeating the process the meaningful value found is -3200 (and -2400). It appears that not only the structure is less stable, but also the solution is. The buckling does show up, which can be seen from the right view.